tensor network for quantum computing

Speaker : Cunxi Gong

Date: 2025-05-23

今日文章

Berezutskii, A.; Acharya, A.; Ellerbrock, R.; Gray, J.; Haghshenas, R.; He, Z.; Khan, A.; Kuzmin, V.; Liu, M.; Lyakh, D.; Lykov, D.; Mandrà, S.; Mansell, C.; Melnikov, A.; Melnikov, A.; Mironov, V.; Morozov, D.; Neukart, F.; Nocera, A.; Perlin, M. A.; Perelshtein, M.; Shaydulin, R.; Villalonga, B.; Pflitsch, M.; Pistoia, M.; Vinokur, V.; Alexeev, Y. Tensor Networks for Quantum Computing. arXiv March 11, 2025. https://doi.org/10.48550/arXiv.2503.08626.

主要作者

作者众多,主要来自工业界

主要作者:
Yuri Alexeev

google scholar
linkedin
nwchem gamess作者之一

量子计算作为21世纪最具颠覆性的技术之一，正在逐步从理论走向实践。

然而，量子系统的模拟和操作面临一个根本性挑战：“维度灾难”（Curse of Dimensionality）。随着量子比特数量的增加，系统的状态空间呈指数级增长，这使得传统的经典计算方法难以高效处理大规模的量子问题。

张量网络（Tensor Networks, TNs） 的引入为解决这一问题提供了强有力的工具。

张量网络最初起源于凝聚态物理中的量子多体问题，用于高效表示低纠缠的量子态。近年来，随着量子信息科学的发展，张量网络的应用范围迅速扩展到量子计算、量子纠错、量子机器学习等多个领域。

这篇文章从张量网络的基本概念出发，系统介绍其在量子计算中的核心应用，包括：

1. 量子计算的模拟：如何用张量网络高效模拟量子算法。
2. 量子电路合成：如何将张量网络转换为实际的量子电路。
3. 量子纠错与错误缓解：张量网络在量子纠错码和解码中的应用。
4. 量子机器学习：张量网络如何提升量子机器学习模型的效率和可解释性。

最后，我们将讨论张量网络在量子计算中的未来发展方向和面临的挑战。

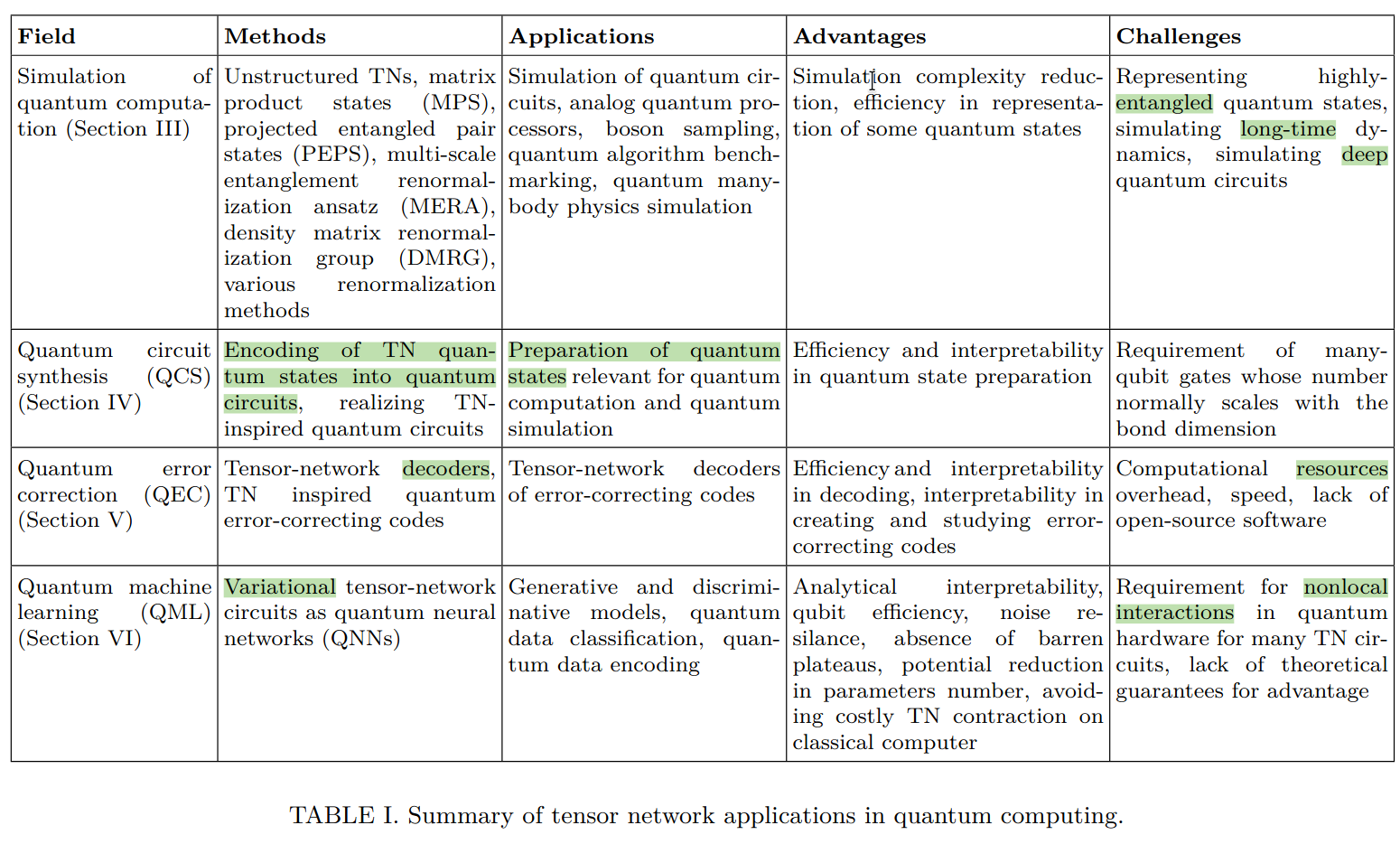
2. 张量网络的基本概念与方法

2.1 张量与张量网络的定义

张量是多维数组的数学抽象，可以看作是向量（一阶张量）和矩阵（二阶张量）的高维推广。在量子力学中，量子态和量子操作都可以表示为张量。

张量网络 是由多个张量通过共享指标（即张量的收缩）连接而成的图结构。例如：

• 矩阵乘积态（MPS）：适用于一维量子系统，通过局部张量的乘积表示全局量子态。
• 投影纠缠对态（PEPS）：适用于二维或更高维系统，能够表示更强的纠缠结构。
• 多尺度纠缠重整化（MERA）：通过分层结构捕捉量子态的多尺度纠缠特性。

2.2 张量网络的核心操作

1. 张量收缩：通过共享指标将多个张量合并为一个新的张量。例如，矩阵乘法是二阶张量的收缩。
2. 张量分解：如奇异值分解（SVD），用于压缩高维张量，降低计算复杂度。
3. 规范变换：通过调整张量的规范形式（如MPS的左/右规范形式），优化计算效率。

2.3 张量网络的图形表示

张量网络通常用图形表示，其中：

• 节点 表示张量。
• 边 表示张量的指标，连接的边表示张量之间的收缩。
  这种表示方法直观且便于计算，尤其在量子电路模拟中广泛应用。
  
  

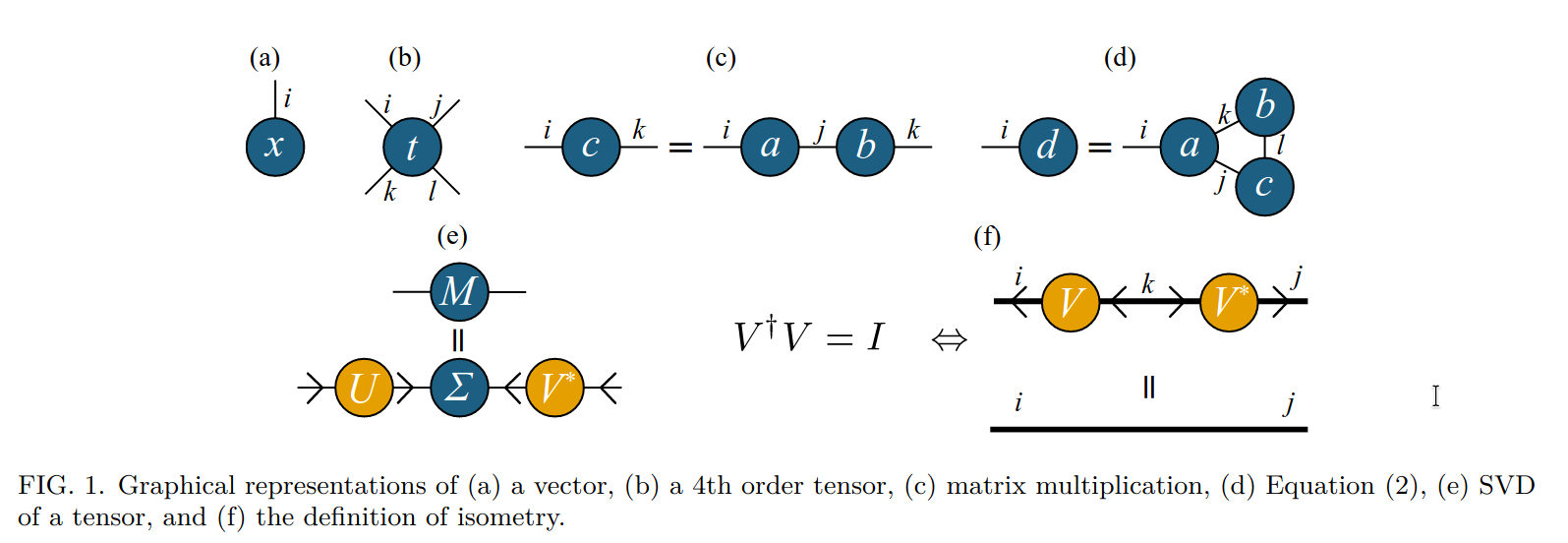
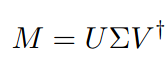
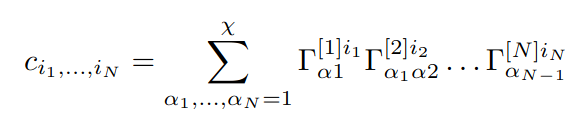
χ is the parameter called the bond dimension which controls the accuracy of compression
This decomposition presents an opportunity for approximate representation of the original tensor by trimming the singular values

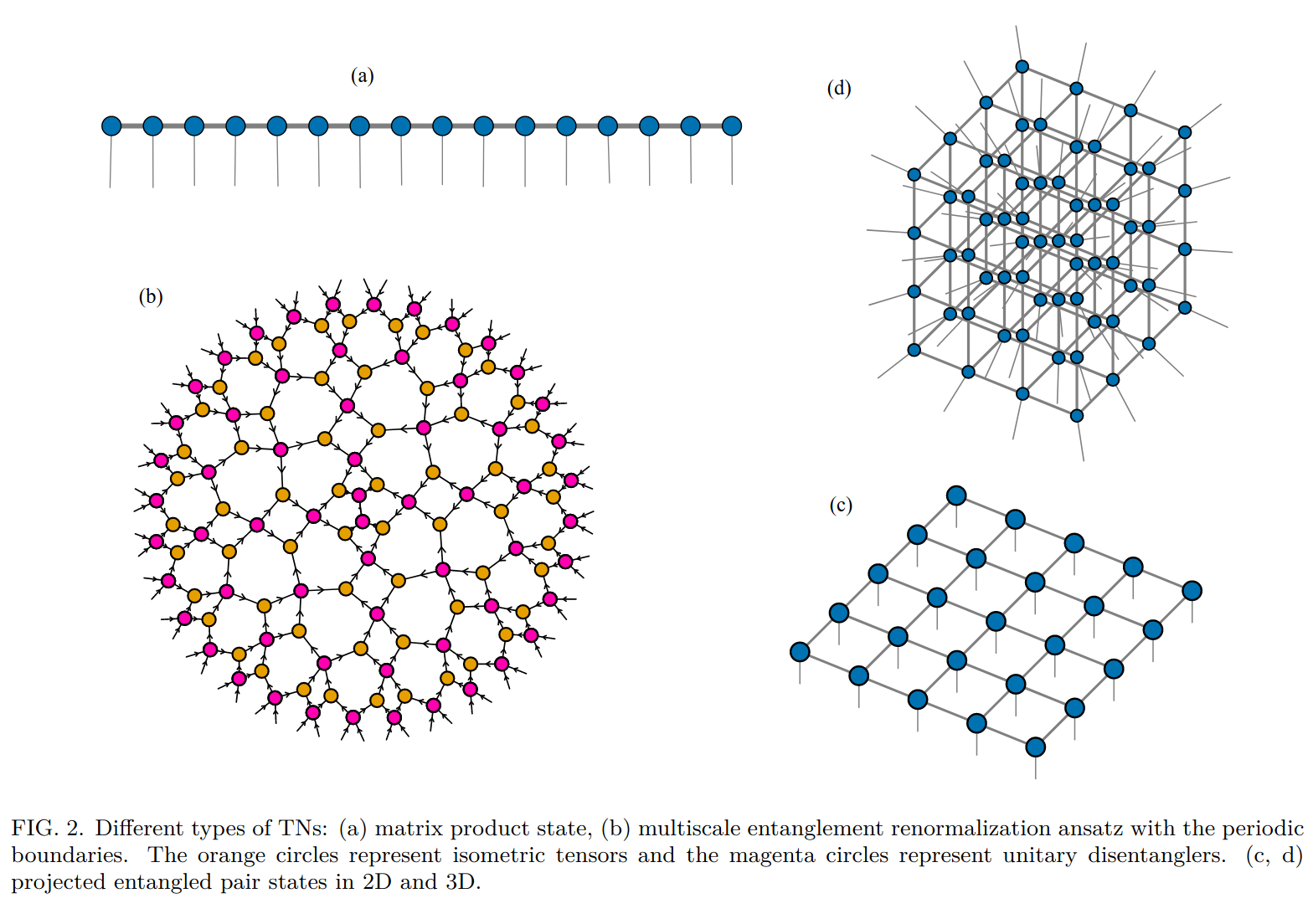
3. 张量网络在量子计算模拟中的应用

3.1 门基量子计算的模拟

量子计算的核心是量子门的操作序列。张量网络可以高效模拟量子电路的演化过程：

• 量子态的表示：将量子态表示为张量网络（如MPS或PEPS），利用其低纠缠特性降低存储需求。
  a quantum state can be represented as a TN of contracted circuit gates with fixed input indices and open output indices

• 量子门的应用：通过局部张量的更新模拟量子门的操作。例如，单量子门作用于MPS中的一个张量，两量子门作用于相邻张量。

案例：随机电路采样（RCS）
随机电路采样是量子优势实验的核心任务。张量网络通过切片（slicing）和近似收缩技术，能够在经典计算机上高效模拟中等规模的量子电路，从而验证量子硬件的性能。

最著名也是很有争议的一个实验

3.2 模拟演化

模拟量子计算机（Analog Quantum Computers）是一种基于连续变量的量子计算形式，其核心思想是通过模拟量子系统的行为来解决计算问题。

量子退火是一种基于绝热定理的优化算法。张量网络可以模拟量子退火过程中的基态演化：

模拟量子模拟器的主要缺点是哈密顿参数的标定误差和量子退相干

• 时间演化算法：如时间演化块解耦（TEBD）和变分时间演化（TDVP），用于模拟量子系统的动力学行为。
• 量子临界现象：张量网络能够捕捉量子相变中的纠缠特性，为实验提供理论指导。

3.3 玻色采样的经典模拟

玻色采样是一种基于线性光学的非通用量子计算模型, 是非常难算的一种模型.

张量网络可以模拟玻色采样.

光子数守恒：对于没有光子损失的情况,利用U(1)对称性压缩张量网络，降低计算复杂度。
因此，使用MPO直接在Fock基中近似混合态是有效的。

4. 张量网络在量子电路合成中的应用

4.1 从张量网络到量子电路

量子电路合成的目标是将抽象的量子操作（如酉算子）转换为实际的量子门序列。

量子电路综合面临两个挑战：
（1）分解算法必须遵守量子器件的原生连通性
（2）允许忠实地准备量子操作的电路深度受到量子器件中特征噪声的限制

张量网络提供了一种系统的方法：

four steps:

1. transforming the original TN into a TN of isometric tensors; 其实就是正则化
2. embedding spatial and temporal directions to the network; 为张量网络分配时间方向，确定量子门的执行顺序
3. promoting each isometric tensor into a unitary; 将每个等距张量提升为酉
4. decomposing each unitary as quantum gates. 分解为单比特和两比特量子门

案例：MPS的量子电路实现
MPS可以通过分层等距变换转换为量子电路，适用于一维量子态的制备。

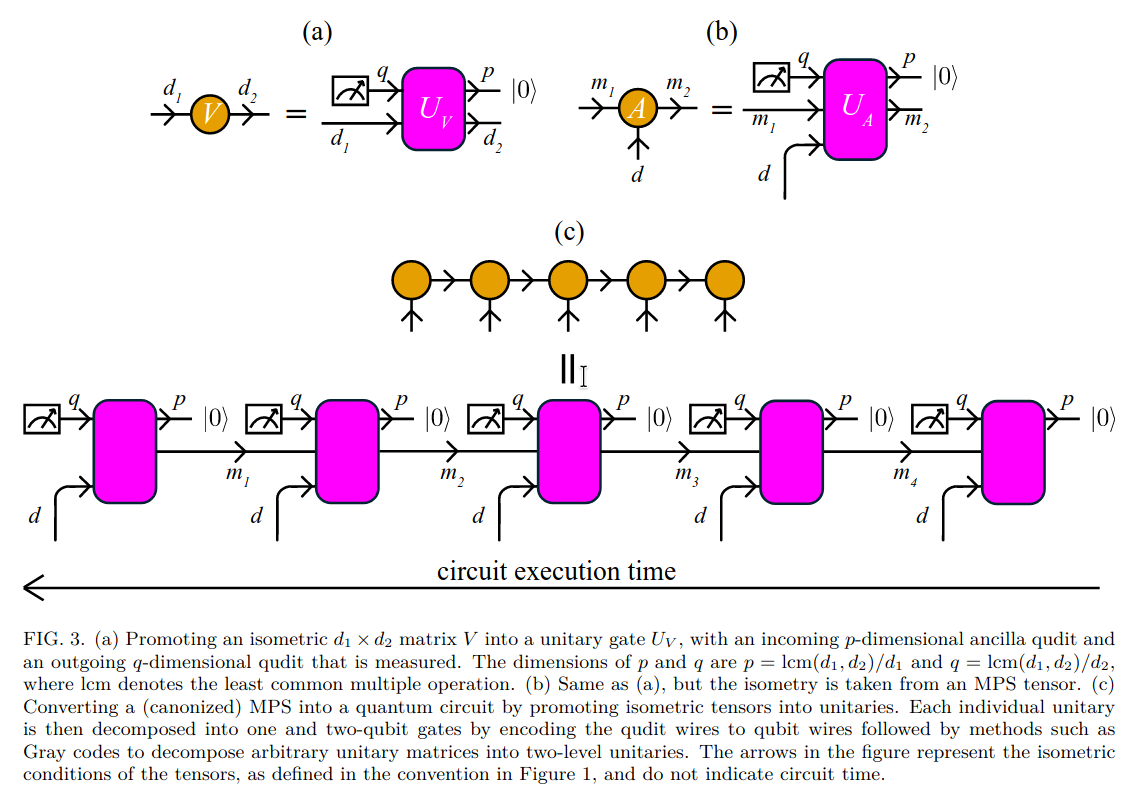
4.2 硬件优化与自适应电路

现代量子硬件的局限性（如有限的连接性和噪声）要求电路设计必须高效。张量网络可以通过以下方式优化：

• 硬件感知合成：根据量子处理器的拓扑结构优化张量网络的收缩顺序。
• 自适应电路：通过中间测量和反馈减少电路深度。

5. 张量网络在量子纠错与错误缓解中的应用

5.1 张量网络编码

量子纠错码（如表面码）可以表示为张量网络：

• 拓扑码的TN表示：PEPS天然适用于二维拓扑码的表示。
• 解码的TN方法：通过张量网络收缩计算最优纠错操作。

5.2 错误缓解技术

在噪声量子设备上，错误缓解技术（如零噪声外推）可以通过张量网络实现：

• 概率错误消除（PEC）：通过准概率分布模拟噪声的反向操作。
• 张量网络错误缓解（TEM）：利用TN收缩降低计算开销。

6. 张量网络在量子机器学习中的应用

6.1 经典机器学习中的张量网络

张量网络已成功应用于经典机器学习任务，如：

• 数据压缩：通过低秩分解减少模型参数。
• 生成模型：如玻尔兹曼机和Born机(生成模型)。

6.2 量子机器学习（QML）

在QML中，张量网络用于：

• 量子数据编码：将经典数据高效嵌入量子态。
• 参数化量子电路：通过TN结构设计高效的量子神经网络（如量子卷积网络）。

7. 未来展望与挑战

7.1 未来方向

• 混合量子-经典计算：张量网络作为经典加速器辅助量子计算。
• 新型TN架构：探索更高效的张量网络结构以适应通用量子计算。

7.2 挑战

• 高维张量网络的收缩复杂度：如何优化高维TN的计算效率。
• 实际硬件的限制：噪声和连接性对TN实现的约束。

8. 结论

张量网络是连接经典计算与量子计算的桥梁，其在模拟线路、合成线路、纠错和机器学习中的应用展现了强大的潜力。随着量子硬件的进步，张量网络将继续推动量子计算从理论走向实用化。未来的研究需要进一步解决计算复杂性和硬件适配性问题，以实现更广泛的量子优势。